Stoichiometric Analysis
Preliminaries
A network of 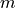 chemical species and
chemical species and 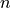 reactions can be described by the
reactions can be described by the
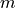 by
by 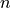 stochiometry matrix
stochiometry matrix 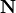 .
. 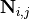 is the net number of
species
is the net number of
species 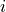 produced or consumed in reaction
produced or consumed in reaction 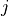 . The dynamics of the network are
described by
. The dynamics of the network are
described by

where  is the vector of species concentrations,
is the vector of species concentrations, 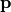 is a vector of time independent parameters, and
is a vector of time independent parameters, and 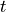 is time.
is time.
Each structural conservation, or interchangably, conserved sum (e.g. conserved moiety) in
the network coresponds to a lineraly dependent row in the stoichiometry matrix 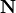 .
.
If there are conserved sums, then the row rank,  of
of 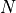 is
is 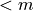 , and
the stochiometry matrix
, and
the stochiometry matrix 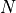 may first be re-ordered such that the first
may first be re-ordered such that the first  are linearly
independent, and the remaining
are linearly
independent, and the remaining 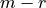 rows are linear combinations of the first
rows are linear combinations of the first  rows. The reduced stochiometry matrix
rows. The reduced stochiometry matrix 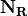 is then formed from the first
is then formed from the first
 rows of
rows of 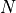 . Finally,
. Finally, 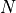 may be expressed as a product of the
may be expressed as a product of the 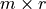 link matrix
link matrix 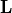 and the
and the 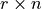
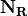 matrix:
matrix:
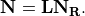
The link matrix 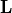 has the form
has the form
![\mathbf{L} = \left[ \begin{array}{c}
\mathbf{I}_{r} \\
\mathbf{L}_0 \end{array} \right],](_images/math/c6977eac5c8c4130105d582c2ef1d2f666ac533a.png)
where 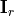 is the
is the 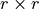 identity matrix and
identity matrix and 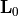 is a
is a 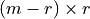 matrix.
matrix.
Full vs. Extended Stoichiometry Matrix
The “full” stoichiometric matrix includes any conserved quantities (as opposed to the reduced stoichiometric matrix, which does not). The extended stoichiometric matrix is equal to the full stoichiometric matrix plus additional rows representing boundary species and sources / sinks. For example, consider the following reaction system:
reaction1: => C
reaction2: C =>
reaction3: C =>
reaction4: MI => M
reaction5: M => MI
reaction6: XI => X
reaction7: X => XI
The extended stoichiometry matrix for this system is:
>>> rr.getExtendedStoichiometryMatrix()
reaction1, reaction2, reaction3, reaction4, reaction5, reaction6, reaction7
C [[ 1, -1, -1, 0, 0, 0, 0],
M [ 0, 0, 0, 1, -1, 0, 0],
X [ 0, 0, 0, 0, 0, 1, -1],
MI [ 0, 0, 0, -1, 1, 0, 0],
XI [ 0, 0, 0, 0, 0, -1, 1],
reaction1_source [ -1, 0, 0, 0, 0, 0, 0],
reaction2_sink [ 0, 1, 0, 0, 0, 0, 0],
reaction3_sink [ 0, 0, 1, 0, 0, 0, 0]]
Methods for Stoichiometric Analysis
The following methods are related to the analysis of the stoichiometric matrix.
RoadRunner::getLinkMatrixRoadRunner::getNrMatrixRoadRunner::getKMatrixRoadRunner::getConservationMatrixRoadRunner::getL0MatrixRoadRunner::getFullStoichiometryMatrixRoadRunner::getExtendedStoichiometryMatrixRoadRunner::getReducedStoichiometryMatrixExecutableModel::getNumConservedMoietiesExecutableModel::getConservedMoietyIdsExecutableModel::getConservedMoietyValuesExecutableModel::setConservedMoietyValues