Steady State Analysis

The dynamics of a biochemical network is described by the system equation

\frac{d}{dt}\mathbf{s}(t) = \mathbf{N} \mathbf{v}(\mathbf{s}(t),\mathbf{p},t),

where

  • \mathbf{s} is the vector of species concentrations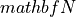

  • mathbf{N} is the stoichiometry matrix

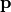  • \mathbf{p} is a vector of time independent parameters

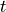  • t is time.

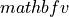  • mathbf{v} is a matrix of reaction fluxes dependent on 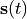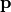\mathbf{s}(t), \mathbf{p} and time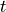 t

The steady state is the solution to the network equations when all the rates of change are zero. That is the concentrations of the floating species, \mathbf{s} that satisfy:

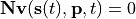
\mathbf{N} \mathbf{v}(\mathbf{s}(t),\mathbf{p},t) = 0

The steady state is easily calculated using the steady state method:

>>> rr.steadyState()
1.234567E-9

The call to steadyState returns a value that represents the sum of squares of the rates of change. Therefore the smaller this value the more likely the steady state solution has been found. Often a value less that 10E-6 indicates a steady state has been found. After a successful call all the species levels will be at their steady state values.

Steady state values can be obtained using rr::RoadRunner::getSteadyStateValues() and :cpp:class::rr::RoadRunner::steadyStateSelections can be used to decide what values to return. For example the following would retrieve a single value:

>>> rr.steadyStateSelections = ['S1']
>>> rr.getSteadyStateValues()
array([ 0.54314239])

One important element in running steady state analysis is the concept of moiety conservation. If the model in question contains moiety conserved cycles, traditional approach to obtain steady state solution fails as it is impossible to calculate the inverse of Jacobian. In such case, we use a walkaround and split the species in a cycle into groups. To do this in RoadRunner, type:

>>> rr.conservedMoietyAnalysis = True

Currently, RoadRunner supports four steady state solvers, nleq2 (the default), nleq1, newton (sundials basic newton) and newton_linesearch (sundials newton with line search globalization).

>>> rr.setSteadyStateSolver('nleq1') # or one of ['nleq2', 'newton', 'newton_linesearch']
>>> solver = rr.getSteadyStateSolver()
>>> solver.settingsPyDictRepr()
"'maximum_iterations': 100, 'minimum_damping': 1e-16, 'relative_tolerance': 0.0001"

To see all available steady state solvers, type:

>>> rr.getRegisteredSteadyStateSolverNames()
('nleq1','nleq2', 'newton', 'newton_linesearch')
The following methods deal with steady state analysis: