Stability Analysis

The stability of a biochemical system is determined by the eigenvalues of the Jacobian matrix. Given 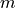$m$ floating species and 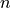$n$ reactions, the Jacobian matrix is defined as follows:

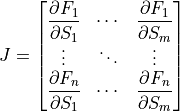
$J=\begin{bmatrix} \dfrac{\partial F_1}{\partial S_1} & \cdots & \dfrac{\partial F_1}{\partial S_m} \\ \vdots & \ddots & \vdots \\ \dfrac{\partial F_n}{\partial S_1} & \cdots & \dfrac{\partial F_n}{\partial S_m} \end{bmatrix}$

where 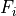$F_i$ is the ith differential equation and 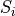$S_i$ the ith floating species. From RoadRunner it is easy to obtain the Jacobian matrix using :cpp:rr::RoadRunner::getFullJacobian, i.e.:

Jac = rr.getFullJacobian()

which returns the Jacobian matrix in the variable Jac.

It is possible for full Jacobian to be singular. In these situations one should call the related method, rr::RoadRunner::getReducedJacobian().