telLevenbergMarquardt.py

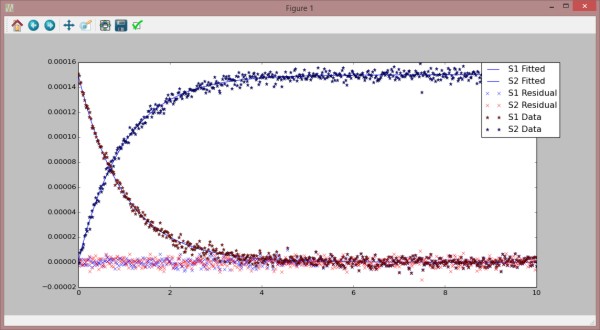
This example demonstrates parameter minimization, using the Levenberg-Marquardt algorithm. Output is shown in the image. To run the example, make sure you have some 'Experimental' data available.

Image output using the example below.

import ctypes
import teplugins as tel

#Get a lmfit plugin object
chiPlugin   = tel.Plugin("tel_chisquare")
lm          = tel.Plugin("tel_levenberg_marquardt")

#========== EVENT FUNCTION SETUP ===========================
def pluginIsProgressing(lmP):
    # The plugin don't know what a python object is.
    # We need to cast it here, to a proper python object
    lmObject = ctypes.cast(lmP, ctypes.py_object).value
    print 'Iterations = ' + `lmObject.getProperty("NrOfIter")` \
        + '\tNorm = ' + `lmObject.getProperty("Norm")`

try:   
    progressEvent =  tel.NotifyEventEx(pluginIsProgressing)
    
    #The ID of the plugin is passed as the last argument in the assignOnProgressEvent. 
    #The plugin ID is later on retrieved in the plugin Event handler, see above
    theId = id(lm)
    tel.assignOnProgressEvent(lm.plugin, progressEvent, theId)
    #============================================================
    #Retrieve a SBML model from plugin        
        
    test_model = tel.readAllText('two_parameters.xml')
    
    #Setup lmfit properties.
    lm.SBML = test_model
    experimentalData = tel.DataSeries.readDataSeries ('ExperimentalData.dat')
    lm.ExperimentalData = experimentalData
    
    # Add the parameters that we're going to fit and a initial 'start' value
    lm.setProperty("InputParameterList", ["k1", 0.8])
    lm.setProperty("InputParameterList", ["k2", 2.3])  
      
    lm.setProperty("FittedDataSelectionList", "[S1] [S2]")
    lm.setProperty("ExperimentalDataSelectionList", "[S1] [S2]")
    
    # Start minimization
    lm.execute()
        
    hessian = lm.getProperty("Hessian")        
    print 'Hessian: \n' + `hessian`
    
    cov = lm.getProperty("CovarianceMatrix")        
    print 'CovarianceMatrix: \n' + `cov`
            
    print 'Minimization finished. \n==== Result ====' 
    print tel.getPluginResult(lm.plugin)
    
    # Get the experimental data as a numpy array
    experimentalData = experimentalData.toNumpy
    
    # Get the fitted and residual data
    fittedData = lm.getProperty ("FittedData").toNumpy
    residuals  = lm.getProperty ("Residuals").toNumpy
    
    tel.telplugins.plot(fittedData         [:,[0,1]], "blue", "-",    "",    "S1 Fitted")
    tel.telplugins.plot(fittedData         [:,[0,2]], "blue", "-",    "",    "S2 Fitted")
    tel.telplugins.plot(residuals          [:,[0,1]], "blue", "None", "x",   "S1 Residual")
    tel.telplugins.plot(residuals          [:,[0,2]], "red",  "None", "x",   "S2 Residual")
    tel.telplugins.plot(experimentalData   [:,[0,1]], "red",  "",     "*",   "S1 Data")
    tel.telplugins.plot(experimentalData   [:,[0,2]], "blue", "",     "*",   "S2 Data")
    tel.telplugins.plt.show()
    
except Exception as e:
    print 'Problem.. ' + `e`