Parameter confidence estimation using the Monte Carlo bootstrap algorithm

Get some confidence estimates

1.1 Introduction

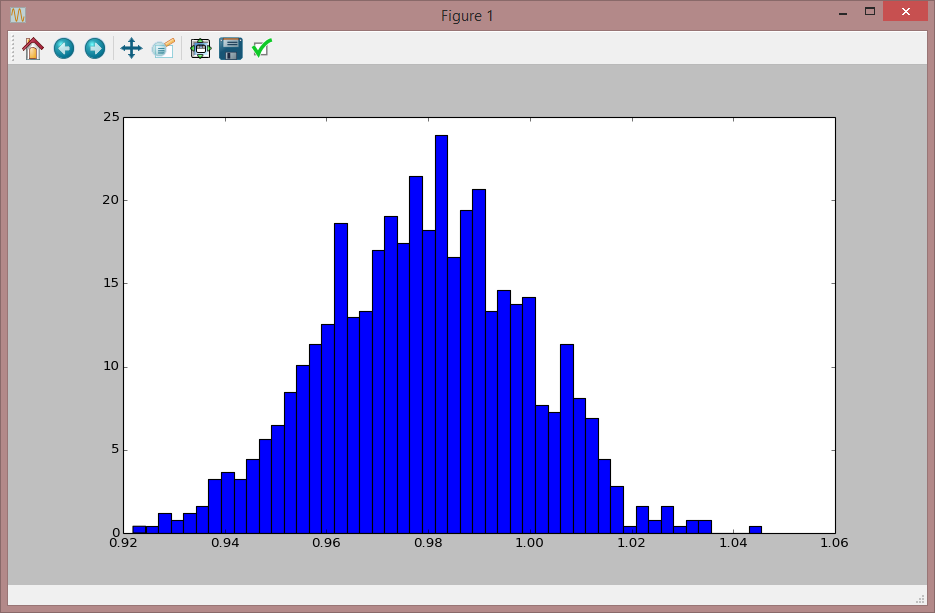
The Monte Carlo plugin is used to obtain estimates of the confidence limits for a model’s parameters. This is in the context where experimental data exists and a parameter minimization method, such as Levenberg-Marquardt or Nelder-Mead has already been used in order to find a parameter minimum.

The Monte Carlo algorithm is used subsequently at this minimum and will give an estimate of parameter confidence limits corresponding to the variance in the original experimental data.

The plugin has properties such as the size of the Monte Carlo population, minimization algorithm to use (e.g. Nelder-Mead or Levenberg-Marquardt), and on output, confidence limits for each involved parameter.

Plugin properties are documented in more detail in the next section.

1.2 Plugin Properties

Available properties in the Monte Carlo plugin are listed in the table below.

Table 1.1: Plugin Properties

Property Name	Data Type	Default Value	Description


SBML	string	N/A	SBML document as a string. Model to be used by the Monte Carlo plugin.
ExperimentalData	telluriumData	N/A	Input data.
InputParameterList	listOfProperties	N/A	Parameters to estimate confidence limits for.
MonteCarloParameters	listOfProperties	N/A	Parameters obtained from a Monte Carlo session.
ConfidenceLimits	listOfProperties	N/A	Confidence limits for each fitted parameter. The confidence limits are calculated at a 95% confidence level.
ExperimentalDataSelectionList	stringList	N/A	Selection list for experimental data.
FittedDataSelectionList	stringList	N/A	Selection list for model data.
NrOfMCRuns	int	N/A	Number of Monte Carlo data sets to generate and use.
MinimizerPlugin	string	N/A	Minimizer used by the Monte Carlo Engine, e.g. ”Levenberg_Marquardt”.

1.3 The execute(bool inThread) function

The execute() function will start the Monte Carlo algorithm. Depending on the problem at hand, the algorithm may run for a long time.

The execute(bool inThread), method supports a boolean argument indicating if the execution of the plugin work will be done in a thread, or not. Threading is fully implemented in the Monte Carlo plugin.

The inThread argument defaults to false.

Each generated Monte Carlo dataset is available in a file named, MCDataSets.dat (saved in current working directory).

1.4 Plugin Events

The Monte Carlo plugin uses all of the available plugin events, i.e. the PluginStarted, PluginProgress and the PluginFinished events.

The available data variables for each event are internally treated as pass through variables, so any data, for any of the events, assigned prior to the plugins execute function (in the assignOn() family of functions), can be retrieved unmodified in the corresponding event function.

Event	Arguments	Purpose and argument types


PluginStarted	void, void	Signal to application that the plugin has started. Both parameters are pass through parameters and are unused internally by the plugin.

PluginProgress	void, void	Communicating progress of fitting. Both parameters are pass through parameters and are unused internally by the plugin.

PluginFinished	void, void	Signals to application that execution of the plugin has finished. Both parameters are pass through parameters and are unused internally by the plugin.

Table 1.2: Plugin Events

1.5 Python example

The following Python script illustrates how the plugin can be used.

1from teplugins import *
2import matplotlib.pyplot as plt
3
4try:
5    #Load plugins
6    modelP      = Plugin("tel_test_model")
7    nP          = Plugin("tel_add_noise")
8    chiP        = Plugin("tel_chisquare")
9    lmP         = Plugin("tel_levenberg_marquardt")
10    nmP         = Plugin("tel_nelder_mead")
11    mcP         = Plugin("tel_monte_carlo_bs")
12
13    #========== EVENT FUNCTION SETUP ===========================
14    def myEventFunction(ignore):
15        # Get the fitted and residual data
16        experimentalData    = lmP.getProperty ("ExperimentalData").toNumpy
17        fittedData          = lmP.getProperty ("FittedData").toNumpy
18        residuals           = lmP.getProperty ("Residuals").toNumpy
19
20        telplugins.plot(fittedData         [:,[0,1]], "blue", "-",    "",    "S1 Fitted")
21        telplugins.plot(fittedData         [:,[0,2]], "blue", "-",    "",    "S2 Fitted")
22        telplugins.plot(residuals          [:,[0,1]], "blue", "None", "x",   "S1 Residual")
23        telplugins.plot(residuals          [:,[0,2]], "red",  "None", "x",   "S2 Residual")
24        telplugins.plot(experimentalData   [:,[0,1]], "red",  "",     "*",   "S1 Data")
25        telplugins.plot(experimentalData   [:,[0,2]], "blue", "",     "*",   "S2 Data")
26
27        print ’Minimization finished. \n==== Result ====’
28        print getPluginResult(lmP.plugin)
29        telplugins.plt.show()
30
31    #Communicating event
32    myEvent =  NotifyEventEx(myEventFunction)
33
34    #Uncomment the event assignment below to plot each monte carlo data set
35    #assignOnFinishedEvent(lmP.plugin, myEvent, None)
36
37    #This will create test data with noise. We will use that as ’experimental’ data
38    modelP.execute()
39
40    #Setup Monte Carlo properties.
41    mcP.SBML                             = modelP.Model
42    mcP.ExperimentalData                 = modelP.TestDataWithNoise
43
44    #Select what minimization plugin to use
45    #mcP.MinimizerPlugin                  = "Nelder-Mead"
46    mcP.MinimizerPlugin                  = "Levenberg-Marquardt"
47    mcP.NrOfMCRuns                       = 100
48    mcP.InputParameterList               = ["k1", 1.5]
49    mcP.FittedDataSelectionList          = "[S1] [S2]"
50    mcP.ExperimentalDataSelectionList    = "[S1] [S2]"
51
52    # Start Monte Carlo
53    mcP.execute()
54
55    print ’Monte Carlo Finished. \n==== Result ====’
56    print mcP.MonteCarloParameters.getColumnHeaders()
57    paras = mcP.MonteCarloParameters.toNumpy
58    print paras
59
60    #Get mean (assuming normal distribution).
61    print "The mean: k1= " + ‘np.mean(paras)‘
62
63
64    PropertyOfTypeListHandle = getPluginProperty(mcP.plugin, "ConfidenceLimits")
65    print ‘getNamesFromPropertyList(PropertyOfTypeListHandle)‘
66    aProperty = getFirstProperty(PropertyOfTypeListHandle)
67    if aProperty:
68        print getPropertyValueAsString(aProperty)
69
70    #Show MOnte Carlo parameters as a histogram
71    plt.hist(paras, 50, normed=True)
72    plt.show()
73
74    #Plot Monte Carlo data sets
75    #dataSeries =  DataSeries.readDataSeries("MCDataSets.dat")
76    #dataSeries.plot()
77
78    #Finally, view the manual and version
79    mcP.viewManual()
80    print ’Plugin version: ’ + ‘mcP.getVersion()‘
81
82
83except Exception as e:
84    print ’Problem.. ’ + ‘e‘

Listing 1.1: Monte Carlo plugin example.

Figure 1.1: Output for the example script above, using 1000 Monte Carlo runs. The histogram shows the distribution for the model parameter, ’k1’. The mean for the distribution was 0.980 and obtained confidence limits were +/- 0.001.